每日题解:LeetCode 84. 柱状图中最大的矩形
2020-05-31
题目描述
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
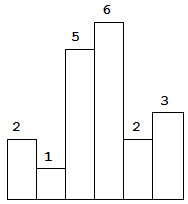
以上是柱状图的示例,其中每个柱子的宽度为 1,给定的高度为 [2,1,5,6,2,3]。
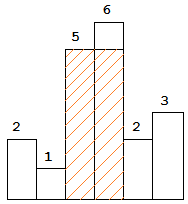
图中阴影部分为所能勾勒出的最大矩形面积,其面积为 10 个单位。
解法
JAVA
public int largestRectangleArea(int[] heights) {
int len = heights.length;
if (len == 0) {
return 0;
}
int ans = 0;
int[] newHeights = new int[heights.length + 2];
System.arraycopy(heights, 0, newHeights, 1, heights.length);
Deque<Integer> stack = new ArrayDeque<>();
for (int i = 0; i < newHeights.length; i++) {
while (!stack.isEmpty() && newHeights[stack.peek()]>newHeights[i]) {
int h = newHeights[stack.pop()];
int left = stack.peek() + 1;
int right = i - 1;
ans = Math.max(ans, (right - left + 1) * h);
}
stack.push(i);
}
return ans;
}
解题思路
暴力
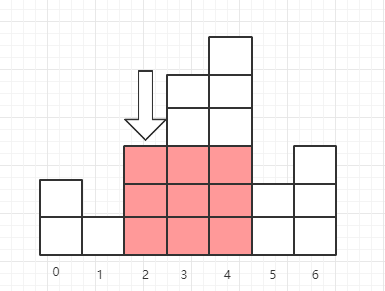
我们可以维护两个指针left、right,两个指针由当前元素往左右扩散
- left指针往左寻找,直到找到大于等于当前元素高度的最左边元素的下标;
- right一个指针往右寻找,直到找到大于等于当前元素高度的最右边元素的下标;
假设当前元素的高度这个矩形的长,则两个指针的距离就是矩形的宽。
int height=heights[i];
//实际的宽度需要加一,如left=5,right=6,之间的距离实际是2
int width = right - left + 1;
-6a65686533d545f6a8c5969713bf1fd2.png)
-9d1c45a74e934f6fbcf559e4a8c40a2b.png)
代码实现
时间复杂度为O(n^2)
int len = heights.length;
//判断,由于题目并没有没有说明heights的长度范围,避免出现NPE
if (len == 0) {
return 0;
}
int ans= 0;
for (int i = 0; i < len; i++) {
//往左寻找
int left = i;
int height = heights[i];
while (left > 0 && heights[left - 1] >= curHeight) {
left--;
}
//往右寻找
int right = i;
//判断是否越界或者找到比他小的元素
while ((right < (len - 1) )&& heights[right + 1] >= height) {
right++;
}
int width = right - left + 1;
ans= Math.max(ans, width * height);
}
return ans;
}
单调栈
使用暴力虽然可以解决这个问题,但是时间的复杂度在O(n^2),很容易出现超时的问题,能不能实现一种单向寻找的解决方法?
我们在第一种解法的图解上继续思考

我们使用一变量记录当前面积的最大值,使用temp数组记录我们待计算面积的下标。
- 当i=0,由于不知道接下来元素的情况,我们暂时记录下,temp[0]为0;
- 当i=1时,当前元素为1,由于heights[0]=2,所以我们可以确定在i=0,最大面积就是2,同时将待计算的面积的下标改为temp[0]=1(0下标,已经计算了)
计算面积heights[0]
int right = 1 - 1;
int left= 0;
int width = right - left + 1;
int height = temp[0];
//更新面积的最大值
ans= Math.max(ans, width * height);
- 当i=2时,当前元素为3,大于上一个元素,此时,我们可以理解为上一个元素暂时没法进行计算面积,同时下标2也无法进行面积的计算,记录emp[0]=1,temp[1]=2
- 当i=3时,当前元素为5,和之前情况类似,记录temp[0]=1,temp[1]=2,temp[3]=3
- 当i=4时,当前元素为6,继续记录temp[0]=1,temp[1]=2,temp[3]=3,temp[4]=6
- 当i=5时,当前元素为2,当前元素小于上一个元素6,我们可以将temp[4]=6,进行计算
- 计算下标为4面积,由于
heights[3]=5 < heights[4]=6,面积为6,更新最大面积值为6,同时删除掉 temp[4],然后temp[3]=3记录下标的值heights[3]=5 < heights[5]=2,可以继续进行计算- 计算下标为3面积,由于
heights[3]=5 < heights[4]=6,理解下的位置上标还有一个为heights[3]=5,计算面积为10,更新最大面积值为10- 以此类推,直到数组记录的坐标没有大于
heights[5]=2
从上面的分析可以直到我们可以计算维护一个依次递增的栈,当前发现下一个元素小于目前栈顶最大的元素,我们就开始进行面积计算
Deque<Integer> stack = new ArrayDeque<>();
for (int i = 0; i < heights.length; i++) {
while (!stack.isEmpty() && heights[stack.peek()]>heights[i]) {
int h = heights[stack.peek()];
int left = stack.poll();
int right = i - 1;
ans = Math.max(ans, (right - left + 1) * h);
}
stack.push(i);
}
}
在debug时,候会发现
遇到[1]、[1,1]的情况会出现问题,都会出现无法对进入循环进,
[1],无法进去循环,不存在 heights[stack.peek()]>heights[i]进行下一个元素的比较
[1,1],最大面积应该是2,无法进行计算最小元素从左到右的面积

这里,我们可以将原数组的长度+2,使得前后添加一个为0的元素,保证可以进入循环
int[] newHeights = new int[heights.length + 2];
//这里,原数组,复制的起始位置,新数组,新数组开始的插入的下标,原数组复制的个数
System.arraycopy(heights, 0, newHeights, 1, heights.length);
Deque<Integer> stack = new ArrayDeque<>();

这样我们记录的一个坐标就是原数起始位置,最后一次计算,我们将计算最小元素从左到右的面积(此时栈顶元素记录坐标为0);由于进行了数组进行了扩容,对于长度为1的数组,我们也可以满足循环的要求heights[stack.peek()]>heights[i],非常巧妙的一个哨兵机制。
玩会扩充并修改原来的循环
for (int i = 0; i < newHeights.length; i++) {
while (!stack.isEmpty() && newHeights[stack.peek()]>newHeights[i]) {
int h = newHeights[stack.pop()];
//有效的数字需要+1
int left = stack.peek() + 1;
int right = i - 1;
ans = Math.max(ans, (right - left + 1) * h);
}
当然可以去掉left 和 right变量
ans = Math.max(ans, ( i - 1- stack.peek()) * h);
