每日题解:LeetCode 990. 等式方程的可满足性
2020-06-08
题目描述
给定一个由表示变量之间关系的字符串方程组成的数组,每个字符串方程 equations[i] 的长度为 4,并采用两种不同的形式之一:"a==b" 或 "a!=b"。在这里,a 和 b 是小写字母(不一定不同),表示单字母变量名。
只有当可以将整数分配给变量名,以便满足所有给定的方程时才返回 true,否则返回 false。
示例 1:
输入:["a==b","b!=a"]
输出:false
解释:如果我们指定,a = 1 且 b = 1,那么可以满足第一个方程,但无法满足第二个方程。没有办法分配变量同时满足这两个方程。
示例 2:
输出:["b==a","a==b"]
输入:true
解释:我们可以指定 a = 1 且 b = 1 以满足满足这两个方程。
示例 3:
输入:["a==b","b==c","a==c"]
输出:true
示例 4:
输入:["a==b","b!=c","c==a"]
输出:false
示例 5:
输入:["c==c","b==d","x!=z"]
输出:true
提示:
1 <= equations.length <= 500
equations[i].length == 4
equations[i][0] 和 equations[i][3] 是小写字母
equations[i][1] 要么是 '=',要么是 '!'
equations[i][2] 是 '='
解法
JAVA
class Solution {
public boolean equationsPossible(String[] equations) {
int[] parent = new int[26];
for (int i = 0; i < 26; i++) {
parent[i] = i;
}
for (String equation : equations) {
//a==b
if(equation.charAt(1)=='='){
int index1 =equation.charAt(0)-97;
int index2 = equation.charAt(3)-97;
//并
union(parent, index1, index2);
}
}
for (String equation : equations) {
//a==b
if(equation.charAt(1)=='!'){
int index1 =equation.charAt(0)-97;
int index2 = equation.charAt(3)-97;
if(findParent(parent,index1)==findParent(parent,index2)){
return false;
}
}
}
return true;
}
private void union(int[] parent, int index1, int index2) {
parent[findParent(parent,index1)]=findParent(parent,index2);
}
public int findParent(int[] parent, int index) {
//查询index的根节点/当(parent[index]=index,说明根节点
while (parent[index] != index) {
parent[index] = parent[parent[index]];
index = parent[index];
}
return index;
}
}
解题思路
并查集
并查集,在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内赛题中,其特点是看似并不复杂,但数据量极大,若用正常的数据结构来描述的话,往往在空间上过大,计算机无法承受;即使在空间上勉强通过,运行的时间复杂度也极高,根本就不可能在比赛规定的运行时间(1~3秒)内计算出试题需要的结果,只能用并查集来描述。
来之百度的描述
我们以 ["a==b","b!=c","c==a"]为例子
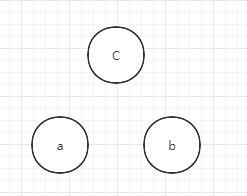
一开始三个独立集合,我能根据==关系连接独立集合
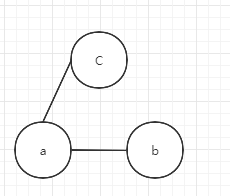
我们查找!=,,"b!=c"由于c==a,a==b,相当于c==b,和"b!=c"冲突返回结构fasle。
我们可以假设a相当于b,c的根节点
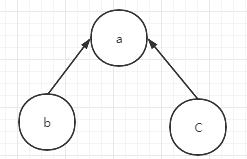
当我们遍历!=条件时,出现两个根节点一致的情况,就认为,当前判断冲突。
//equations[i][0] 和 equations[i][3] 是小写字母,我们就直接建立一个26字母的数组
int[] parent = new int[26];
for (int i = 0; i < 26; i++) {
parent[i] = i;
}
并
for (String equation : equations) {
//a==b 字符长度为4,其中1下标为'=',标志是"=="
if(equation.charAt(1)=='='){
//转换为26字母范围内
int index1 =equation.charAt(0)-97;
int index2 = equation.charAt(3)-97;
//并
union(parent, index1, index2);
}
}
并方法
private void union(int[] parent, int index1, int index2) {
//这里涉及查找直接伪代码写法
parent[index1的根节点的值]=index2的根节点
}
查
for (String equation : equations) {
//a==b
if(equation.charAt(1)=='!'){
int index1 =equation.charAt(0)-97;
int index2 = equation.charAt(3)-97;
//查找两个下标的根节点是否相同,相同就返回false,与之前的规则冲突
if(findParent(index1根节点)==findParent(index2根节点)){
return false;
}
}
}
实现查找的方法
public int findParent(int[] parent, int index) {
//查询index的根节点,当(parent[index]=index,说明根节点
while (parent[index] != index) {
//继续遍历直到查找根节点
parent[index] = parent[parent[index]];
index = parent[index];
}
//返回根节点的下标
return index;
}
替换掉并的查找方法
private void union(int[] parent, int index1, int index2) {
parent[find(parent,index1)]=find(parent,index2);
}