每日题解:LeetCode 面试题29. 顺时针打印矩阵
2020-06-05
题目描述
输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字。
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
示例 2:
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]
限制:
0 <= matrix.length <= 100
0 <= matrix[i].length <= 100
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/shun-shi-zhen-da-yin-ju-zhen-lcof
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解法
JAVA
class Solution {
public int[] spiralOrder(int[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return new int[0];
}
int column = matrix[0].length;
int row = matrix.length;
int left = 0;
int top = 0;
int right = column - 1;
int under = row - 1;
int[] res = new int[column * row];
int index = 0;
while (left <= right && top <=under) {
//输出上
for (int i = left; i <=right ; i++) {
res[index++]=matrix[top][i];
}
//输出右
for (int i = top+1; i <=under ; i++) {
res[index++]=matrix[i][right];
}
if (left < right && top < under) {
//输出下
for (int i = right - 1; i > left; i--) {
res[index++] = matrix[under][i];
}
//输出左
for (int i = under; i > top; i--) {
res[index++] = matrix[i][left];
}
}
left++;
right--;
top++;
under--;
}
return res;
}
}
CPP
class Solution {
private:
static constexpr int directions[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
if (matrix.size() == 0 || matrix[0].size() == 0) {
return {};
}
int columns = matrix[0].size();
int rows = matrix.size();
//返回结果
int total = rows * columns;
vector<int> res(total);
vector<vector<bool>> visited(rows, vector<bool>(columns));
//遍历数组
int row = 0;
int column = 0;
int index=0;
for (int i = 0; i < total; i++) {
res[i]= matrix[row][column];
visited[row][column] = true;
//计算下一个坐标位置
int nextRow = row + directions[index][0];
int nextColumn = column + directions[index][1];
//判断是否越界
if(nextRow < 0 || nextRow >= rows
|| nextColumn < 0 || nextColumn >= columns ||visited[nextRow][nextColumn]){
//越界修改方向
//4次方向后,恢复到0
index = (index + 1) % 4;
}
row += directions[index][0];
column += directions[index][1];
}
return res;
}
};
解题思路
今天的c和java分别是两种思路的写法,JAVA的写法按照层次顺序从外到内进行输出,c则是模拟了题目描述,顺时针的输出。
层次
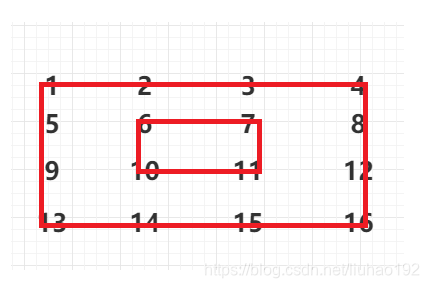
如图,我们按照外圈和内圈的顺序输出数组的元素,每个圈的输出顺序为分为上,右,下,左的顺序,我们用四个变量标记四个顶点的值。
int column = matrix[0].length;
int row = matrix.length;
int left = 0;
int top = 0;
int right = column - 1;
int under = row - 1;
//返回结果
int[] res = new int[column * row];
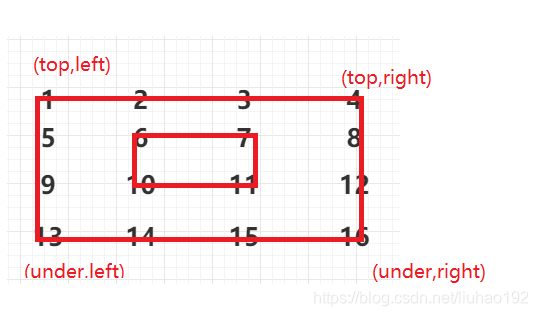
我们分开输出
上
从(top,left)=>(top,right)
其中left增加,top不变
for (int i = left; i <=right ; i++) {
res[index++]=matrix[top][i];
}
右
从(top,right)=>(unde,right)
其中top增加,right不变,由于(top,right)已经遍历过了,直接从top+1开始
for (int i = top+1; i <=under ; i++) {
res[index++]=matrix[i][right];
}
下
从(unde,right)=>(unde,left)
其中right减少,under不变,由于(unde,right)已经遍历过了,直接从 right - 1开始
for (int i = right - 1; i > left; i--) {
res[index++] = matrix[under][i];
}
左
从(unde,left)=>(top,left)
其中under减少,left不变,在上一个循环我们没输出(unde,left)这个点,这里我们从(unde,left)开始
for (int i = under; i > top; i--) {
res[index++] = matrix[i][left];
}
外圈遍历结束后我们需要缩小范围到内容,从图可以看出
left++;
right--;
top++;
under--;
那么我们结束的条件什么 ?就是中间那个点, 这个点属于中心位置,left = right && top =under,所以
while (left <= right && top <=under) {
}
然后组装代码,提交测试
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return new int[0];
}
int column = matrix[0].length;
int row = matrix.length;
int left = 0;
int top = 0;
int right = column - 1;
int under = row - 1;
int[] res = new int[column * row];
int index = 0;
while (left <= right && top <=under) {
//输出上
for (int i = left; i <=right ; i++) {
res[index++]=matrix[top][i];
}
//输出右
for (int i = top+1; i <=under ; i++) {
res[index++]=matrix[i][right];
}
//输出下
for (int i = right - 1; i > left; i--) {
res[index++] = matrix[under][i];
}
//输出左
for (int i = under; i > top; i--) {
res[index++] = matrix[i][left];
}
left++;
right--;
top++;
under--;
}
return res;
当我们庆贺的时候,

可以,那就加条件判断(没注意长度>=0)
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return new int[0];
}
再次提交,测试

官方的测试用例干的漂亮!!!
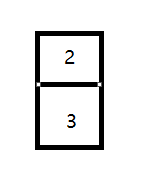
用例是这个结构
我们能输出上,右,但是输出下的时候,会出现下标出界的问题,此时需要再输出下和左的时候需要加一个判断
//只有left<right和top<under的时候才进行遍历。这里可以结合图像思考,left<right说明至少横线至少有两个,
top<under纵向也是至少两个,2*2的结构才能绕圈进行输出
if (left < right && top < under) {
}
顺序输出
模拟输出的顺序如图
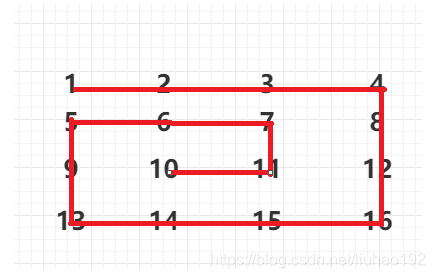
主要思路在四个点的位置怎么变动方向?
一开始我采用了判断的思路,到了边界进行转向的判断,后来看到了大佬的思路
static constexpr int directions[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
int index=0;
......
if 到底边界
index = (index + 1) % 4;
一开始index是0,我们从从(top,left)=>(top,right),left每次加1,当到底边界的时候,我们index+1,对4取模,我们从数组的下标1,开始(top,right)=>(unde,right),top每次加1,依次类推知道我们触碰四次边界的时候,再次取模后index恢复到0,真的太巧妙。
vector<vector<bool>> visited(rows, vector<bool>(columns));
使用二维数组记录遍历过的记录,当我们在内部的模拟的时候,可以判断是否到达边界。
这里没对模拟的具体的描述,主要在转向和是否达到边界的这两块。个人还是喜欢层次遍历, 思路比较明确!!
按照惯例今天,带来了源码一个骚操作
System.out.println(16*0.75);
System.out.println( 16 - (16 >>> 2));
对的这么1.8的ConcurrentHashMap,计算扩容阈值的操作